Decibel serves as the universal unit for measuring sound intensity, capturing a diverse range of sounds that humans can detect. The dB is everywhere, from adjusting sound levels on your headphones to measuring the noise level in a factory. This logarithmic unit of intensity measurement is essential for representing both large and small quantities.
Knowing how to calculate decibels is essential for evaluating signal strength, sound level, and the efficient designing of audio systems. This guide will help you calculate decibels with clarity, enabling you to make informed and data-driven decisions.
What is a Decibel?
The decibel (dB) is a logarithmic unit used to measure the intensity of sound or relative power by comparing it with a given reference point. It doesn’t provide an absolute value, but it indicates how much stronger or weaker one value is compared to the other. It’s based on the ratio of a particular sound to the quietest sound that the human ear can detect, known as the “threshold of hearing.”

Generally, it refers to the degree of loudness and is widely used in signals, telecommunications, and the electronics industry. Because it uses logarithmic units, it displays numerical data of different values based on the power of 10.
What is the Decibel Scale?
The human ear has a built-in mechanism that reduces its sensitivity to rising sound levels and handles a diverse range of sound power levels. Therefore, the ear can distinguish between two pins dropping, but it cannot distinguish higher-decibel sounds because the human ear is not linear.

On the decibel scale, the quietest possible sound, also known as near-silent sound, is 0 dB. However, a sound ten times more powerful is 10 dB, 100 times more potent than the near-silent is 20 dB, and so on. With every ten decibels, sound intensity increases significantly, and sounds above 85 dB become hazardous to our ears.
How to calculate decibels?
Calculating decibels involves understanding the logarithmic relationship between two values and expressing these ratios on a scale. As decibels are relative to the specific reference value, applying the correct formula depends on the type of measurement you are working with. Below is the complete process for calculating decibels using the appropriate formula.
Identifying the Type of Measurement
The first step is identifying the type of quantity you are working with. Applying the correct formula is crucial for obtaining accurate results, especially in decibel calculations, which are based on logarithmic ratios rather than arithmetic.
Power-based Measurements
The basic form of decibel calculations involves comparing two power levels, which is equivalent to ten times the logarithm of the power for its reference point. In the power-based formula, the multiplier is always 10, and standard units are Watts (W) and milliwatts (mW).
Voltage or Current Measurements
Although the decibel is primarily used for comparing power levels, current or voltage equations can be used if the provided impedance levels are the same. So, the voltage ratio formula applies when comparing electrical voltages or signal levels.
Sound Pressure Measurements
In acoustics, the standard method for measuring sound pressure level is to use sound level meters or microphones. It’s used for measuring noise levels and for designing soundproof systems. A small “p” denotes it, and the units are Pascals (Pa) or microPascals (mPa).
Apply the Correct Formula
As the decibel calculations are logarithmic, they express ratios between two quantities, and the formula you use depends on what value you are comparing.
For Power Measurements
For power measurements such as electrical power or signal strength, the decibel formula will be:
10 log (P2 / P1) dB
Where P2 is the output power level
P1 is the input power level or reference point
For instance, if both values have similar elements, such as frequency, there will be no difference because the sound intensity from them is the same. However, if the output is twice compared to the reference point, the difference will be:
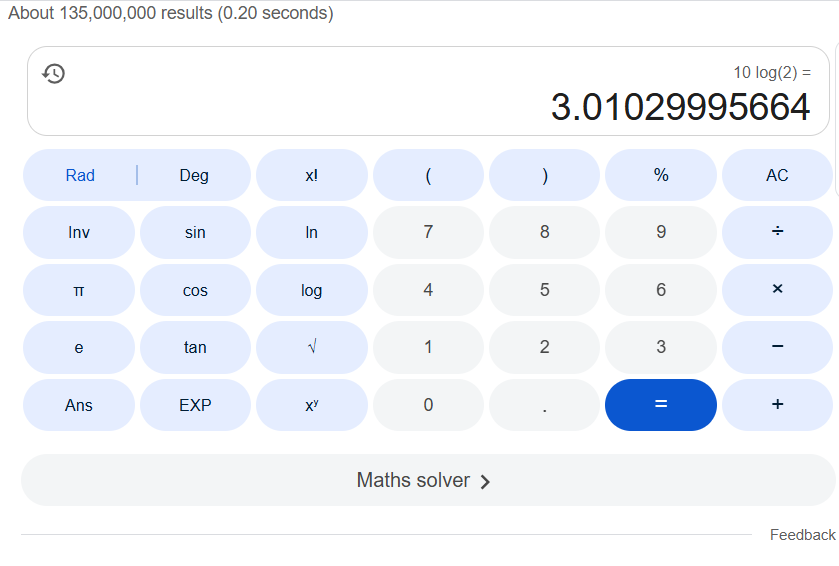
10log (10 watts/ 5 watts)
= 10 log 2 =3 dB
It means the power has increased by 3 decibels. Similarly, if the power is 100 times more powerful than the other, then:
10 log (P2 / P1) dB
= 10 log 100
= 20dB
It means the difference in sound will be 20 dB if the stronger sound is 100 times louder than the other.
For Voltage or Current
If the impedance remains constant across two power levels, then the power is directly proportional to the square of the voltage. So, voltage can be expressed in dB by the following formula:
=10 log (V22 / V12)
It can be written simply as:
= 20 log (V2 / V1) = 20 log (I2 /I1)
Where V2 is the output voltage or current, and V1 is the input voltage or reference point. For instance, if an amplifier receives a 1-watt signal and produces a 100-watt signal, then the gain will be:
= 10 log (100 /1)
= 20 dB
It shows a 20-decibel increase in signal level.
For Sound Pressure Level
In acoustic measurements, such as speaker output or noise level, the decibel value is calculated using sound pressure and a fixed reference. Since the sound energy is proportional to the square of the pressure, the logarithmic value can be written as:
SPL (dB)=20 log 10 (p /pref)
p = measure sound pressure (in Pascals)
pref = fixed 20 µPa (threshold of human hearing)
Decibel Shortcuts and Special Abbreviations
Decibel Abbreviations
In technical fields such as telecommunications and electronics, you often see decibel values with suffixes like dBW, dBV, or dBm. These abbreviations serve as shortcuts to show the type of reference point used in the calculation. Therefore, understanding them is crucial to calculating and interpreting the data correctly.
| Abbraviations | Reference Value /Usage |
| dBm | Power level of approximately 1 mW |
| dBW | Power level is approximately 1 watt |
| dBV | Level concerning 1 volt |
| dBA | “A” weighted sound pressure or sound intensity measurement. |
| dBC | C-weighted decibel scale for peak sound pressure in industrial settings |
| dBi | Gain of an antenna in communication concerning an isotropic source |
Decibel Shortcuts
Most of the time, you can estimate the dB values of common ratios without needing the calculator. By memorizing a few frequently used values, you can efficiently handle most practical situations.
| Power Ratio | dB Value | Voltage Ratio | dB Value |
| 0.001 | -30 | 0.001 | -60 |
| 0.01 | -20 | 0.01 | -40 |
| 0.1 | -10 | 0.1 | -20 |
| 1 | 0 | 1 | 0 |
| 2 | 3 | 2 | 6 |
| 4 | 6 | 4 | 12 |
| 5 | 7 | 5 | 14 |
Common Mistakes to Avoid when Calculating Decibels
Calculating decibels is straightforward, but due to the logarithmic and reference values involved, errors can arise that lead to significant inaccuracies. Below are common mistakes to avoid when calculating decibels:
Incorrectly Adding or Subtracting dB Values
Generally, the error occurs when attempting to directly add or subtract dB values without converting them to a linear scale. Since decibels are logarithmic, to combine power levels, convert the dB value to a linear scale (in watts or milliwatts), perform the addition or subtraction, and then convert it back to decibels.
Neglecting the Reference Value
Decibels are used to express ratios, and neglecting or using incorrect reference values makes the decibel value meaningless. For instance, if the “sound level is 80 dB,” then the reference value is crucial to understanding it. If it’s 20 μPa, an 80-decibel sound level would indicate a sound level above the threshold of hearing.
Ignoring Environmental Factors
Failing to account for prominent environmental factors, such as reflections or distance, can lead to inaccurate assessments. For example, sound pressure levels decrease with distance, and reflections can either mask or amplify specific sounds.
Improper Use of Logarithmic Functions
Decibel calculations utilize base-10 algorithms, and using a base-e (natural) algorithm can yield incorrect dB values.
Conclusion
Calculating decibels is essential across various fields, such as audio engineering and telecommunications, as it utilizes a logarithmic scale. Therefore, it allows you to represent large or small ratios in a more manageable way, but it requires precision. By understanding the measurement type and the correct reference value, you can ensure accurate results.
By applying the correct method and avoiding common mistakes, you can accurately calculate decibels to enhance the quality and performance across various audio fields.
FAQs
Can decibels be used to measure things other than sound?
Yes, decibels are used to measure more than sound. They are a logarithmic unit for expressing ratios between two quantities, often used to measure sound, and apply to various fields, including electronics, electrical engineering, and signal processing.
Why do decibels not follow a linear scale?
Decibels use a logarithmic scale because the human auditory response to sound intensity is logarithmic. It means the perception of loudness changes slowly as sound intensity increases. Moreover, a logarithmic scale allows you to represent large or small ratios in a compact and manageable way.
Is there a difference between analog and digital dB measurements?
Yes, both are different. Analog dB refers to continuous signals and is used with units like dBV to describe signal levels, which can exceed 0 dB. In digital dB measurements, the standard is dBFS, where zero dBFS represents the maximum level.
Are decibel measurements affected by distance?
Yes, decibel measurements are significantly affected by the distance from the sound source. The measured sound level decreases as you move further away from the source. The sound intensity drops by 6 dB every time the distance is doubled in an open environment.

































.png)
.png) Français
Français .png) Deutsch
Deutsch .png) Italiano
Italiano .png) 日本語
日本語 .png) Português
Português  Español
Español